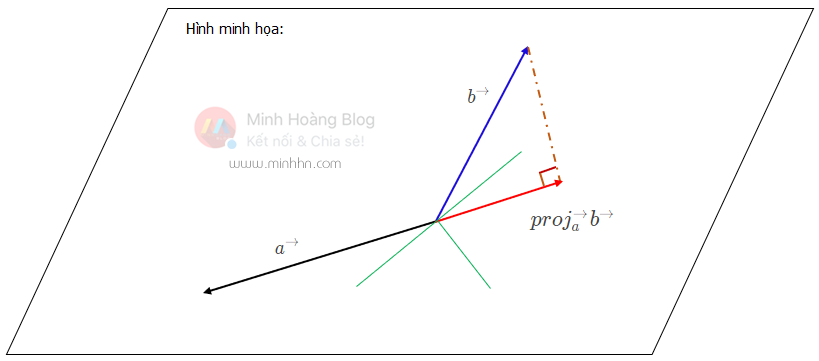
Để tìm hình chiếu của vector b^→ lên vector a^→ bằng cách sử dụng tích vô hướng (dot product) theo công thức sau:
proj_a^→b^→ = (\frac{b^→・a^→}{||a^→||^2})a^→ = (\frac{b_1a_1 + b_2a_2 + b_3a_3}{(\sqrt {{ a_1 }^{ 2 } + { a_2 }^{ 2 } + { a_3 }^{ 2 }})^2})a^→
Ví dụ:
Giả sử chúng ta có 2 vector a^→ = (-1,5,-2) và vector b^→ = (0,-4,-2). Tìm hình chiếu của vector b^→ lên vector a^→
Sử dụng công thức trên chúng ta có:
proj_a^→b^→ = (\frac{(0,-4,-2)・(-1,5,-2)}{(\sqrt {{(-1)}^{2} + {(5)}^{2} + {(-2)}^{2}})^2})(-1,5,-2)
= (\frac{(0 * -1) + (-4 * 5) + (-2 * -2)}{(\sqrt {30})^2})(-1,5,-2)
= (\frac{-20 + 4}{(\sqrt {30})^2})(-1,5,-2)
= (\frac{-16}{30})(-1,5,-2)
= (\frac{-8}{15})(-1,5,-2)
= (\frac{8}{15},\frac{-8}{3},\frac{-16}{15})
Như vậy, kết quả vector hình chiếu của vector b^→ lên vector a^→ là: proj_a^→b^→ ≈ (0.53,-2.37,-1.07)
Có thể bạn quan tâm:
– Cách tìm độ lớn của một vector.
– Dot product (Tích vô hướng) – Tính góc giữa hai vector.
Cảm ơn bạn đã theo dõi. Đừng ngần ngại hãy cùng thảo luận với chúng tôi!









[…] thể bạn quan tâm: – Vector hình học và các khái niệm về vector. – Tìm hình chiếu của một vector lên một vector khác sử dụng Dot Product. – Cộng và trừ vector hình […]
[…] thể bạn quan tâm: – Vector hình học và các khái niệm về vector. – Tìm hình chiếu của một vector lên một vector khác sử dụng Dot Product. – Tìm hình chiếu của một vector lên một mặt phẳng thông qua vector pháp […]