Cộng và trừ vector hình học

Số lượng vô hướng có thể được cộng hoặc trừ bằng cách tính toán đại số thông thường. Ví dụ, 4kg đường và 3kg đường, khi kết hợp với nhau bằng mọi cách, luôn cho 7kg đường, hay khi bạn trừ thì luôn nhận được 1kg đường. Điều này không phải lúc nào cũng có trong trường hợp vector, vì ngoài độ lớn chúng còn có hướng nữa. Trong bài viết này, chúng ta cùng tìm hiểu cách cộng và trừ vector hình học. Khi 2 vector được cộng hoặc trừ, thì kết quả sẽ tạo ra một vector.

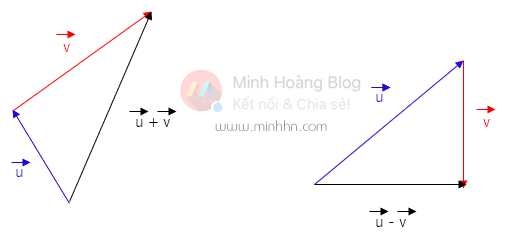
Chúng ta có 2 vector u^→ = (u_1, u_2) và v^→ = (v_1, v_2)

• Cộng 2 vector u^→ + v^→ = (u_1 + v_1, u_2 + v_2)
• Trừ 2 vector u^→ - v^→ = u^→ + (-v^→) = (u_1 - v_1, u_2 - v_2)

Vector kết quả của cộng hoặc trừ hai vector có thể được tìm thấy bằng phương pháp hình bình hành (parallelogram method) hoặc phương pháp tam giác (triangle method).

1. Phương pháp hình bình hành (parallelogram method)

• Vẽ các vector sao cho các điểm ban đầu của chúng trùng nhau.
• Sau đó vẽ các đường thẳng để tạo thành một hình bình hành hoàn chỉnh.
• Đường chéo từ điểm ban đầu đến đỉnh đối diện của hình bình hành là vector kết quả.

■ Cộng 2 vector u^→, v^→

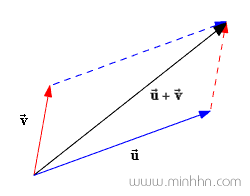
■ Trừ 2 vector u^→, v^→

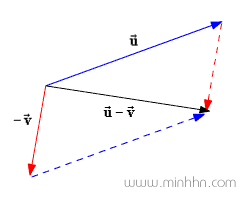
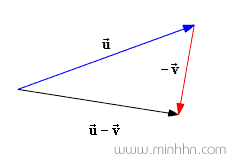
2. Phương pháp tam giác (triangle method)

• Vẽ các vector lần lượt, đặt điểm đầu của mỗi vector kế tiếp tại điểm cuối của vector trước đó.
• Sau đó vẽ kết quả từ điểm ban đầu của vector đầu tiên đến điểm cuối của vector cuối cùng, chúng ta sẽ được vector kết quả.
• Phương pháp này còn được gọi là phương pháp từ đầu đến đuôi.

■ Cộng 2 vector u^→, v^→

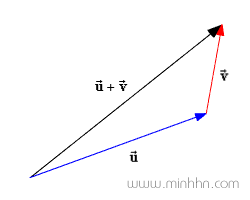
■ Trừ 2 vector u^→, v^→

Ví dụ:

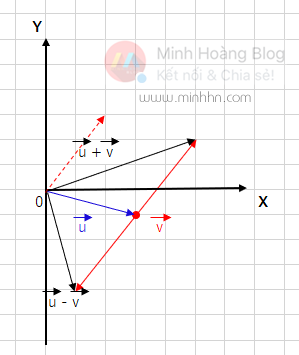
Tính cộng và trừ 2 vector u^→ = (3, -1) và v^→ = (2, 3)

● Cộng 2 vector u^→ + v^→ = (3 + 2, -1 + 3) = (5, 2)

● Trừ 2 vector u^→ - v^→ = (3 - 2, -1 - 3) = (1, -4)

Có thể bạn quan tâm:
– Dot product (Tích vô hướng) – Tính góc giữa hai vector.
– Tích vector – Cross product (Tích hữu hướng).

Cảm ơn bạn đã theo dõi. Đừng ngần ngại hãy cùng thảo luận với chúng tôi!