Giả sử chúng ta đã có các giá trị sau:
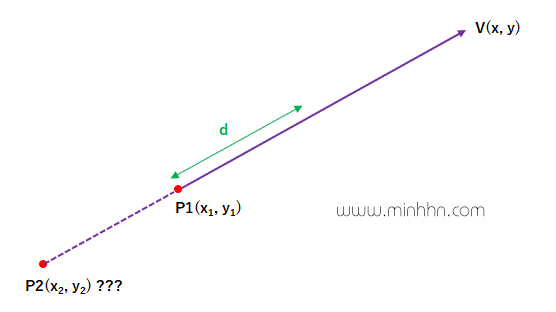
- Một vector V^→(x, y)
- Một điểm P1(x_1, y_1) nằm trên vector V^→
- Một khoảng cách d từ điểm P1 đến điểm cần tìm P2(x_2, y_2) cũng nằm trên vector V^→

Để tính được tọa độ của điểm P2(x_2, y_2) thì chúng ta làm như sau:
#1/2:
Chuẩn hóa (normalize) vector V^→ thành vector đơn vị (là vector có độ dài bằng 1) U^→ = \frac{V^→}{||V^→||}
Trong đó:
- Độ dài (cũng là độ lớn) của vector V^→(x, y) được xác định (define) là ||V^→||=\sqrt {{ x }^{ 2 } + { y }^{ 2 }}.
- Và \frac{V^→}{||V^→||} có nghĩa là: (\frac { x }{ \sqrt {{ x }^{ 2 } + { y }^{ 2 }} } , \frac { y }{ \sqrt {{ x }^{ 2 } + { y }^{ 2 }} }), các điểm cùng hướng với V^→ và có độ dài đơn vị (unit length).
Ví dụ: nếu V^→ = (3, 4), thì U^→ = (\frac { 3 }{ 5 },\frac { 4 }{ 5 })
- Một vector đi qua 2 điểm này bằng công thức: V^→(x, y) = (x_2, y_2) − (x_1, y_1). Ví dụ: nếu P1 = (0, 0) và P2 = (3, 4), thì V^→ = (3, 4)
- Khoảng cách giữa điểm bắt đầu P1(x_1, y_1) và điểm kết thúc P2(x_2, y_2) được xác định bằng công thức: d = \sqrt {{(x_2 - x_1)}^{ 2 } + {(y_2 - y_1)}^{ 2 }}
#2/2:
Sử dụng công thức vector: P2 = P1 + d * U^→
Trong đó:
- P2 là tọa độ của điểm cần tìm.
- P1 là tọa độ của điểm bắt đầu.
- d là khoảng cách từ P1 đến P2.
- U^→ là tọa độ của vector đã được chuẩn hóa.
※Nếu dùng công thức P2 = P1 – d * U^→ thì tọa độ điểm P2 sẽ theo hướng ngược lại.
Có thể bạn quan tâm:
– Vector hình học và các khái niệm về vector.
– Tìm hình chiếu của một vector lên một vector khác sử dụng Dot Product.
– Tìm hình chiếu của một vector lên một mặt phẳng thông qua vector pháp tuyến.








Em rất thích những bài về Geometry của anh. Anh cho thể chia sẻ tài nguyên anh đã học để có những kiến thức này ko ạ
Em cám ơn anh
Kiến thức toán học thôi em, anh memo lại để dùng khi cần.