Các vector được sử dụng để biểu diễn một đại lượng có cả độ lớn (magnitude) và hướng (direction). Hướng của vector là từ đuôi (tail) đến đầu (head) của nó. Các vector thường được trực quan hóa trong một biểu đồ. Một vector giữa A và B được viết là: AB^→
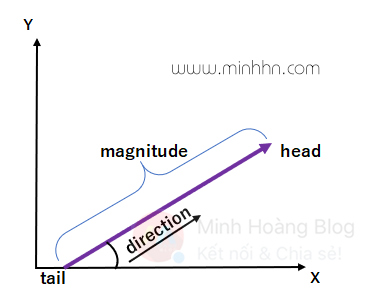
1. Độ lớn (magnitude) của vector
Độ lớn của vector AB^→(x, y) viết là ||AB^→||. Được xác định bằng: ||AB^→|| = \sqrt {{ x }^{ 2 } + { y }^{ 2 }}
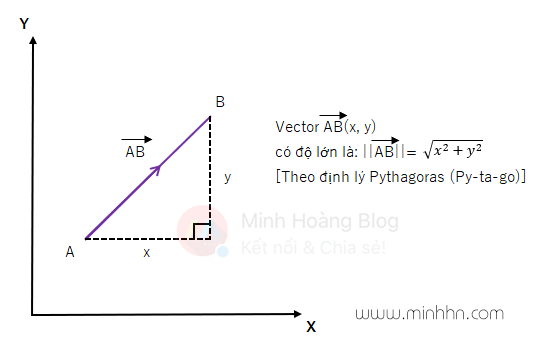
Ngoài ra, độ lớn của vector AB^→ cũng chính là khoảng cách từ điểm bắt đầu A đến điểm kết thúc B. Do đó, nếu biết được tọa độ của điểm A(x_1, y_1) và B(x_2, y_2) thì chúng ta có thể sử dụng công thức tính khoảng cách (distance formula) giữa 2 điểm AB để tính độ lớn của vector: ||AB^→|| = \sqrt {{(x_2 - x_1)}^{ 2 } + {(y_2 - y_1)}^{ 2 }}
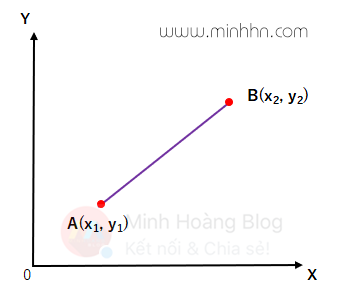
2. Hướng (direction) của vector
Hướng của vector là số đo của góc mà nó tạo với một đường nằm ngang (horizontal line).
Chúng ta có thể sử dụng 1 trong 2 công thức sau đây để tìm hướng của vector:
- Giả sử chúng ta có vector V^→, có tọa độ là (x, y) thì hướng của vector V^→ được tính bằng tanθ = \frac { y }{ x }
- Trường hợp vector được tạo bởi 2 điểm điểm A(x_1, y_1) và B(x_2, y_2) thì hướng của vector AB^→ được tính bằng tanθ = \frac{y_2 - y_1}{x_2 - x_1} ⇒ θ = { tan }^{ -1 }(\frac{y_2 - y_1}{x_2 - x_1}), kết quả thu được θ có đơn vị tính bằng độ ° \left( 0° \le θ \le 180° \right).
Ví dụ:
Tìm hướng của vector AB^→ có điểm đầu A(2,3) và điểm cuối B(5,8).
Với tọa độ của các điểm đầu, cuối đã được xác định, chúng ta thay thế vào công thức tanθ = \frac{y_2 - y_1}{x_2 - x_1}
tanθ = \frac{8 - 3}{5 - 2} = \frac{5}{3}
Tìm tan nghịch đảo để tính được góc của θ = { tan }^{ -1 }(\frac{5}{3}) ≈ 59°
Vector AB^→ có hướng khoảng 59°
3. Hai vector bằng nhau
Hai vector được gọi là bằng nhau nếu chúng có cùng độ lớn và hướng. Điều này có nghĩa là nếu chúng ta lấy một vector và dịch nó sang một vị trí mới (không xoay nó), thì vector chúng ta thu được ở cuối quá trình này là cùng một vector chúng ta có lúc đầu.
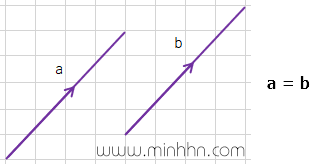
4. Zero vector và unit vector
Một vector có độ lớn 0 được gọi là vector không (zero vector), được viết là 0.
Một vector có độ lớn 1 được gọi là vector đơn vị (unit vector).
5. Nghịch đảo (inverse) vector
Nghịch đảo của một vector là một vector có độ lớn bằng nhau nhưng theo hướng ngược lại.
Nghịch đảo của vector AB^→ là -AB^→ hoặc BA^→, nghịch đảo của của a^→ là -a^→.
Tìm nghịch đảo của một vector thì đơn giản chúng ta thêm dấu – cho tọa độ của vector ban đầu, tức là lấy tọa độ của vector ban đầu nhân với -1.
Ví dụ:
Vector AB^→(3, 4) thì vector nghịch đảo của nó là -AB^→ hoặc BA^→ có tọa độ là (-3, -4)
6. Vector vô hướng (Scalar vector)
Vector vô hướng có độ lớn nhưng không có hướng. Các vector có thể được nhân với một vô hướng (scalar) để tạo ra một vector khác.
7. Nhân vector với một số
Nhân vector X^→ với 3 sẽ cho một vector mới gấp 3 lần chiều dài và song song với X^→.









[…] Xem thêm: Cách tính độ lớn của một vector. […]
[…] Xem thêm: Cách tính độ lớn của một vector. […]
[…] thể bạn quan tâm: – Cách tìm độ lớn của một vector. – Dot product (Tích vô hướng) – Tính góc giữa hai […]
[…] thể bạn quan tâm: – Vector hình học và các khái niệm về vector. – Tìm hình chiếu của một vector lên một vector khác sử dụng Dot Product. […]
[…] thể bạn quan tâm: – Cách tìm độ lớn của một vector. – Dot product (Tích vô hướng) – Tính góc giữa hai […]